1 注意力机制
Transformer模型完全基于注意力机制,因此要了解Transformer就得先知道什么是注意力机制。
1.1 注意力提示
在人类的感知过程中,我们不会平均地处理所有信息,而是会有选择地聚焦于与当前任务最相关的部分。
注意力机制(Attention Mechanism)正是借鉴了这种思维方式,使模型在处理输入序列时能够动态地“分配注意力”。
首先来看一个例子:
- “我吃了一个苹果。”
- “苹果发布了新产品。”
当我们读到“吃了一个苹果”时,会更关注“吃”这个动作,从而推断“苹果”是水果;
当我们读到“苹果发布了新产品”时,会关注“发布”和“产品”,于是知道“苹果”指的是公司。
注意力提示就是根据我们现在的需要对不同的词赋予不同的权重,来让模型聚焦于当前任务中最重要的那部分。
在注意力机制中,这个“聚焦”过程由三个向量表示:
- 查询(Query):当前要处理的元素(例如“苹果”)
- 键(Key):输入序列中其他元素的表示(如“吃”,“发布”等)
- 值(Value):每个输入元素对应的语义信息
1.2 注意力汇聚
查询和键之间的交互形成了注意力汇聚; 注意力汇聚有选择地聚合了值(感官输入)以生成最终的输出。
Nadaraya-Watson 核回归是注意力汇聚的一个经典例子,可以更好的理解注意力机制是如何工作的。
首先我们来看这样一个回归问题,任务是学习一个$f(x)$来预测任意新输入$x$的输出$\hat{y}=f(x)$

当我们想预测x=2时候的输出,最简单的办法就是找到训练样本中x在2附近的几个样本求他们的平均值如果只选取左右两个点做平均,也可能看作是线性插值。
不管怎么选取,你都会发现,此时我们的“注意力”都落在了x附近的样本上。
这里选取x附近的5个点平均值的作为预测输出


主要看右边的热力图,每一行对应一个test_x的输出时候的权重,可以看到每个x都选取了5个train_y,并且权重都是0.2
也就是前面说的将x附近的5个点平均值的作为预测输出
test_x 是 Query,每一行注意力权重对应这个 Query 对训练样本 train_y(Value)的加权分配。
可以看到,注意力机制让 Query 聚焦在与其最相关的训练样本附近,这就是注意力汇聚的直观体现。
如果我们希望让每个训练样本都对预测值有贡献,但距离越近权重越大,而距离远的样本影响越小,该怎么做呢?
为了更平滑地聚合所有训练样本,我们可以使用 Nadaraya-Watson核回归(NW 回归)。
NW 回归会根据距离对训练样本加权,距离越近权重越大,距离越远权重越小:
$$ f(x) = \sum_{i=1}^n \frac{K(x - x_i)}{\sum_{j=1}^n K(x - x_j)} y_i, $$
这里的核函数 $K(u)$ 可以是高斯核:
$$ K(u) = \frac{1}{\sqrt{2\pi}} \exp(-\frac{u^2}{2}) $$
可以看到,这和我们刚才的注意力机制一样:每个 Query 对应一个权重分布,通过加权求和得到最终输出。


$$f(x) = \sum_{i=1}^n \alpha(x, x_i) y_i$$
上面的NW回归是固定参数的,数据量不够大,所以拟合的效果不是很好
我们可以直接对距离乘个系数,甚至可以把这个系数当成可以学习的参数,然后对其进行训练,这就是带参数注意力汇聚。
1.3 注意力评分函数
在Nadaraya-Watson核回归中,我们把高斯核代入后,可以得到: $$ \begin{split}\begin{aligned} f(x) &=\sum_{i=1}^n \alpha(x, x_i) y_i\\ &= \sum_{i=1}^n \frac{\exp\left(-\frac{1}{2}(x - x_i)^2\right)}{\sum_{j=1}^n \exp\left(-\frac{1}{2}(x - x_j)^2\right)} y_i \\ &= \sum_{i=1}^n \mathrm{softmax}\left(-\frac{1}{2}(x - x_i)^2\right) y_i. \end{aligned}\end{split} $$ 把这个过程分成两部分,先算$-\frac{1}{2}(x - x_i)^2$,得到$x$和每个元素$x_i$的距离,因为有个负号,这个值越小说明距离越远,然后把这个函数的输出结果输入到softmax函数中进行运算,将得到与键对应的值的概率分布(即注意力权重)。 最后,注意力汇聚的输出就是基于这些注意力权重的值的加权和。
可以发现重点就是$-\frac{1}{2}(x - x_i)^2$这个式子,他决定了每个键-值对的权重占比,因此可以把这一部分视为注意力评分函数(attention scoring function)。
我们把这个函数记作$a(\mathbf{q}, \mathbf{k}_i)$,
它衡量了$\mathbf{q}$和第$i$个键$\mathbf{k}_i$的相关性,是一个标量;而$\mathbf{q}$会跟每一个键$k$都计算得到一个相关性评分
但是此时的分布可能是比较随机的,不能直接当权重来用
因此我们再做一次softmax,就可以把每一个评分转成一个0~1的值,且刚好每个键的所有权重加起来是1。
因为我们后面只考虑Query和单个Key的值,所以就不再对Key进行索引了,直接用$\mathbf{k}$表示,即$a(\mathbf{q}, \mathbf{k})$。
你可能对$\mathbf{q}$和$\mathbf{k}$的长度感到疑惑,其实这个长度根据任务不同是不一样的:
- 对于前面的回归问题,$\mathbf{q}$和$\mathbf{k}$都只是标量
- 在自然语言处理中,$\mathbf{q}$和$\mathbf{k}$可能是矢量,以此来表示语义信息
意味着$\mathbf{q}$和$\mathbf{k}$可能是不同长度的矢量的,
我们再来重新看一下评分函数,其实它就是把这两个矢量映射成标量,
而根据评分函数映射方式的不同,我们可以把注意力分成加性注意力和缩放点积注意力。
1.4 加性注意力
加性注意力(additive attention)的评分函数为: $$ a(\mathbf q, \mathbf k) = \mathbf w_v^\top \text{tanh}(\mathbf W_q\mathbf q + \mathbf W_k \mathbf k) \in \mathbb{R}, $$
这里的$\mathbf W_q \in \mathbb R^{h\times q}$、$\mathbf W_k \in \mathbb R^{h\times k}$和$\mathbf w_v \in \mathbb R^{h}$都是可学习的参数
其实它就是把任意长度的$\mathbf q$和$\mathbf k$先分别映射成长度为h的矢量,然后把他们加起来,这样就把Query和Key联系起来了,接着再用tanh作为激活函数,然后再用$\mathbf w_v$进一步把长度为h的矢量映射成标量。
因为$\mathbf q$和$\mathbf k$的长度没有限制,因此当查询和键是不同长度的矢量时,一般使用加性注意力作为评分函数。
1.5 缩放点积注意力
缩放点积注意力(scaled dot-product attention)评分函数为: $$ a(\mathbf q, \mathbf k) = \mathbf{q}^\top \mathbf{k} /\sqrt{d} $$ 由于其只需要计算一次矩阵乘法,因此计算效率更高,但是点积操作要求查询和键有相同的长度d。
但是如果只是单纯的相乘,就会有个问题:
假设查询和键的所有元素都是均值为0方差为1的独立随机变量,那么元素个数为d时点积的方差就会变成d,
当$d$较大时,点积结果分布会非常分散,输入 softmax 后容易出现梯度消失或数值不稳定的问题。
因此需要除以$\sqrt{d}$来缩放方差,使其与向量维度无关,稳定训练。
class DotProductAttention(nn.Module):
"""缩放点积注意力"""
def __init__(self, dropout, **kwargs):
super(DotProductAttention, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
# queries的形状:(batch_size,查询的个数,d)
# keys的形状:(batch_size,“键-值”对的个数,d)
# values的形状:(batch_size,“键-值”对的个数,值的维度)
# valid_lens的形状:(batch_size,)或者(batch_size,查询的个数)
def forward(self, queries, keys, values, valid_lens=None):
d = queries.shape[-1]
# 设置transpose_b=True为了交换keys的最后两个维度
scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)
1.6 自注意力机制
自注意力机制就是$Q,K,V$ 都是输入序列$X$吗?对,但不完全对。
我们先来看看会有什么问题:
同一个 $x_i$ 既要用于计算相似度,又要携带语义内容。
模型无法灵活调整哪些特征维度用于匹配、哪些用于表达信息。
因此,引入三个可学习的线性变换来得到查询(Q)、键(K)、值(V):
$$
Q = W^Q X, \quad K = W^K X, \quad V = W^V X
$$
这里的 $X \in \mathbb{R}^{d_{model} \times n}$ 是输入序列, $W^Q, W^K, W^V$ 是可学习的参数矩阵。
它们把同一个输入映射到三个不同的子空间:
- Query 空间:表示“我想关注谁”
- Key 空间:表示“我是谁,能被谁匹配”
- Value 空间:表示“我能提供什么信息”
然后计算: $$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{Q^\top K}{\sqrt{d_k}}\right)V $$
这样就能让序列中的每个位置(token)都能与同一序列中的其他位置交互,从而捕获全局依赖关系。
1.7 多头注意力机制
只用一组 $W^Q, W^K, W^V$,模型在同一组映射下只能学习一种“关注模式”,
但在自然语言中,不同词之间往往存在多种类型的关系。
多头注意力机制就是并行地执行多次独立的注意力计算,每个注意力头在不同的子空间中学习不同的关系。
每个注意力头$\mathbf{h}_i$($i = 1, \ldots, h$)的计算方法为:
$$\mathbf{h}_i = f(\mathbf W_i^{(q)}\mathbf q, \mathbf W_i^{(k)}\mathbf k,\mathbf W_i^{(v)}\mathbf v) \in \mathbb R^{p_v}$$
其中,可学习的参数包括 $\mathbf W_i^{(q)}\in\mathbb R^{p_q\times d_q}$、 $\mathbf W_i^{(k)}\in\mathbb R^{p_k\times d_k}$和 $\mathbf W_i^{(v)}\in\mathbb R^{p_v\times d_v}$, 以及代表注意力汇聚的函数$f$。
然后把每个头的输出拼接起来,再经过另一个线性转换: $$\mathbf W_o \begin{bmatrix}\mathbf h_1\\vdots\\mathbf h_h\end{bmatrix} \in \mathbb{R}^{p_o}$$ 因此其可学习参数是 $\mathbf W_o\in\mathbb R^{p_o\times h p_v}$
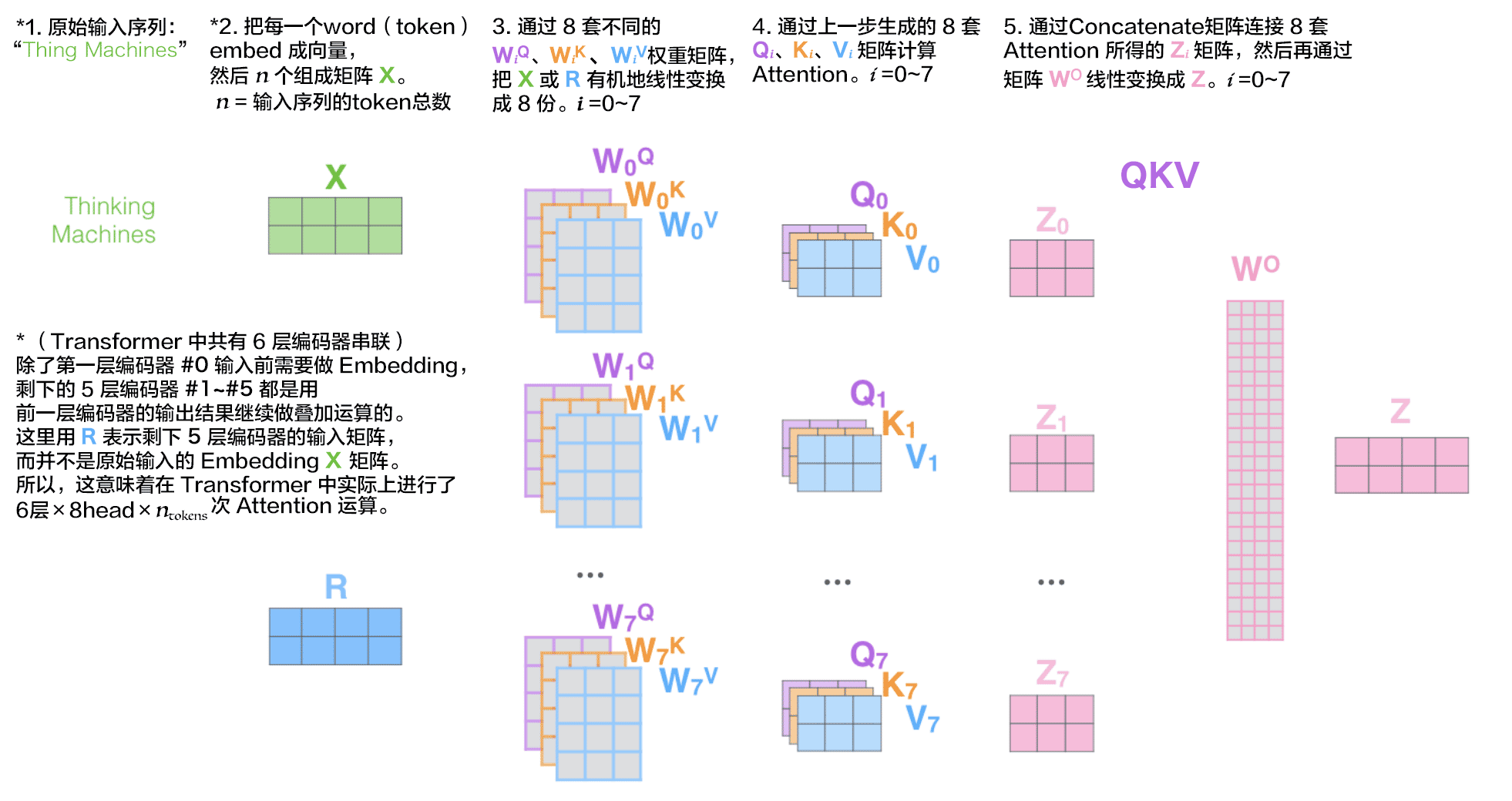
用原来的方法映射到多个Q、K、V,其实这一步还没有涉及到多头注意力机制的核心,
因为这时候把$W_1到W_7$竖着拼起来得到的结果就是对应Q、K、V下标从0~7竖着拼起来。
真正和单头注意力机制区分开来的地方是在点积缩放注意力:
单头注意力机制就只对一组大的Q、K、V做一次点积缩放注意力,
而多头注意力机制是对好几组Q、K、V分别做点积缩放注意力。
在后面具体实现的时候,通过适当的张量操作,可以实现多头注意力的并行计算,从而大幅加快计算速度。
1.8 掩码(Mask)
Transformer中的Mask主要有两种作用:Padding Mask和Sequence Mask。
Padding Mask用于处理不同长度的序列,通过将填充(padding)部分的影响置零,避免其干扰模型计算。
在批处理(batch)训练时,为了使所有序列长度一致,会将较短的序列在末尾填充(padding)。这些填充部分没有实际意义,不应参与注意力计算。Padding Mask通过在计算注意力分数时,将填充位置的权重设为负无穷,使其经过softmax后权重接近于零,从而忽略这些位置的信息。在计算Loss时不让padding token对Loss产生梯度
Sequence Mask用于在解码过程中阻止模型看到未来的信息,确保模型在生成某个词时,只能依赖于之前已生成的词。
sequence mask有各种各样的形式和设计,最常见的应用场景是在需要一个词预测下一个词的时候,如果用self attention 或者是其他同时使用上下文信息的机制,会导致模型”提前看到“待预测的内容,这显然不行,所以为了不泄露要预测的标签信息,就需要 mask 来“遮盖”它。
训练的任务不同,mask的方法也不同,比如BERT就是随机地掩盖每个序列中15%的token,并不是像word2vec中的cbow那样去对每一个词都进行预测。MLM从输入中随机地掩盖一些词,其目标是基于其上下文来预测被掩盖单词的原始词汇。
2 Transformer模型
Transformer模型完全基于注意力机制,最初是应用在文本数据上的序列到序列的学习,后来也推广到图像、音频等领域。
2.1 模型概览
Transformer是由编码器和解码器组成的,其编码器和解码器是基于注意力的模块叠加而成的,在输入序列和输出序列进入编码器和解码器之前,先进行嵌入表示转换成向量,再进行位置编码。
2.2 嵌入层
在NLP任务中,我们往往需要把自然语言的输入转化为向量,这样可以将含义相近的词映射到距离相近的语义空间。
Embedding 层其实是一个存储固定大小的词典的嵌入向量查找表。在输入神经网络之前,我们往往会先让自然语言输入通过分词器 tokenizer,分词器的作用是把自然语言输入切分成 token 并转化成一个固定的 index,然后通过这个index去索引得到该token的词向量。
Embedding 内部是一个可训练的权重矩阵,其行数等于输入词表的大小(vocab_size),列数等于特征向量的维度(embed_size)。词表里的每一个值,都对应一行维度为 embed_size 的向量。
对于输入的值,会对应到这个词向量,然后拼接成(batch_size,seq_len,embed_size)的矩阵输出。
self.embedding = nn.Embedding(vocab_size, embed_size)
2.3 位置编码
在处理词元序列时,循环神经网络是逐个的重复地处理词元的, 而自注意力则因为并行计算而放弃了顺序操作。
为了使用序列的顺序信息,通过在输入表示中添加 位置编码(positional encoding)来注入绝对的或相对的位置信息。
假设输入$\mathbf{X} \in \mathbb{R}^{n \times d}$表示一个序列含有n个词元,每个词元用d维向量表示。
位置编码使用相同形状的位置嵌入矩阵$\mathbf{P} \in \mathbb{R}^{n \times d}$,
矩阵第i行、第2j列和2j+1列上的元素为:
$$
\begin{split}\begin{aligned} p_{i, 2j} &= \sin\left(\frac{i}{10000^{2j/d}}\right)\
p_{i, 2j+1} &= \cos\left(\frac{i}{10000^{2j/d}}\right)\end{aligned}\end{split}
$$
用 sin 和 cos 交替,可以让模型通过线性组合轻松计算“两个位置之间的相对位移”。推导略。
class PositionalEncoding(nn.Module):
"""位置编码"""
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# 创建一个足够长的P
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(10000, torch.arange(
0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)
2.4 多头自注意力
和1.7 多头注意力机制基本类似,主要讲代码实现和通过张量操作实现多头注意力的并行计算。
Transformer使用了8组不同的QKV,也就是使用了8个注意力头,正常计算的话,对于每个头,都需要单独的三个线性层,变换成三个QKV矩阵,单独进行8次缩放点积注意力运算,然后把这8次计算得到的结果拼接起来,再经过一个线性层得到输出Z。
这些线性层不同头之间可以合并起来,所以其实不需要3*8个线性层,我们可以把不同头的QKV权重矩阵拼接起来,这样只需要三个大的权重矩阵。
然后可以通过一些张量操作,先改变张量形状,只通过一次运算得到全部结果,再把形状变回去。这样的好处是这8个注意力头可以实现并行计算。
为了实现上述过程需要借助这两个函数:
def transpose_qkv(X, num_heads):
"""为了多注意力头的并行计算而变换形状"""
# 输入X的形状:(batch_size,查询或者“键-值”对的个数,num_hiddens)
# 输出X的形状:(batch_size,查询或者“键-值”对的个数,num_heads,num_hiddens/num_heads)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
# 输出X的形状:(batch_size,num_heads,查询或者“键-值”对的个数, num_hiddens/num_heads)
X = X.permute(0, 2, 1, 3)
# 最终输出的形状:(batch_size*num_heads,查询或者“键-值”对的个数, num_hiddens/num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
def transpose_output(X, num_heads):
"""逆转transpose_qkv函数的操作"""
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
return X.reshape(X.shape[0], X.shape[1], -1)
transpose_qkv的输入参数X是输入矩阵经过三个线性变换后得到的QKV,目的就是把num_heads和batch_size合并到同一个维度。 做完attention后,再变换回去 transpose_output就是transpose_qkv反转操作。
下面我们来实现多头自注意力机制
class MultiHeadAttention(nn.Module):
"""多头注意力"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = DotProductAttention(dropout)
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
# queries,keys,values的形状:
# (batch_size,查询或者“键-值”对的个数,num_hiddens)
# valid_lens 的形状:
# (batch_size,)或(batch_size,查询的个数)
# 经过变换后,输出的queries,keys,values 的形状:
# (batch_size*num_heads,查询或者“键-值”对的个数,num_hiddens/num_heads)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
if valid_lens is not None:
# 在轴0,将第一项(标量或者矢量)复制num_heads次,然后如此复制第二项,然后诸如此类。
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# output的形状:(batch_size*num_heads,查询的个数,num_hiddens/num_heads)
output = self.attention(queries, keys, values, valid_lens)
# output_concat的形状:(batch_size,查询的个数,num_hiddens)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
if valid_lens is not None,说明有做mask,不是整句做attention,如果复制的话,形状对不上!
因为多头注意力把 batch 在头的维度上复制了 num_heads 倍,所以 mask(valid_lens)也必须复制,否则形状对不上。
2.5 层归一化与残差连接
使用LayerNorm而不是BatchNorm,主要是因为:
- BatchNorm 的归一化依赖 batch 统计,而 NLP 序列有 padding、变长、batch 小, 导致 BN 均值/方差失真和不稳定;
- LayerNorm 基于每个 token 自身特征归一化,不依赖 batch → 更稳定、更好用。
class AddNorm(nn.Module):
"""残差连接后进行层规范化"""
def __init__(self, normalized_shape, dropout, **kwargs):
super(AddNorm, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
self.ln = nn.LayerNorm(normalized_shape)
def forward(self, X, Y):
return self.ln(self.dropout(Y) + X)
X是原始输入,Y是经过attention之后的输出,self.ln(self.dropout(Y) + X)就是残差连接。
2.6 基于位置的前馈网络
前馈网络其实就是MLP,而之所以叫基于位置的,是因为这个MLP是单独作用于每个位置内部的,并且不同位置使用的是同一组权重;
他的作用其实就是对每个token(不太准确,因为这个token已经通过attention混合了其他token的信息)内部的特征维进行一个非线性变换。
需要注意的是,MLP只会对我们输入矩阵的最后一个维度进行变换,
例如我们有个X形状是(批量大小,时间步数或序列长度,隐单元数或特征维度),那我们MLP的输入维度就要求为隐单元数或特征维度;
而MLP的输出维度数量ffn_num_outputs,就会导致我们输入的X形状变成(批量大小,时间步数或序列长度,ffn_num_outputs)。
实现:
class PositionWiseFFN(nn.Module):
"""基于位置的前馈网络"""
def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs,
**kwargs):
super(PositionWiseFFN, self).__init__(**kwargs)
self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
self.relu = nn.ReLU()
self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)
def forward(self, X):
return self.dense2(self.relu(self.dense1(X)))
2.7 编码器-解码器架构
transformer是一种典型的编码器解码器架构,也有纯用编码器或者纯用解码器的模型。
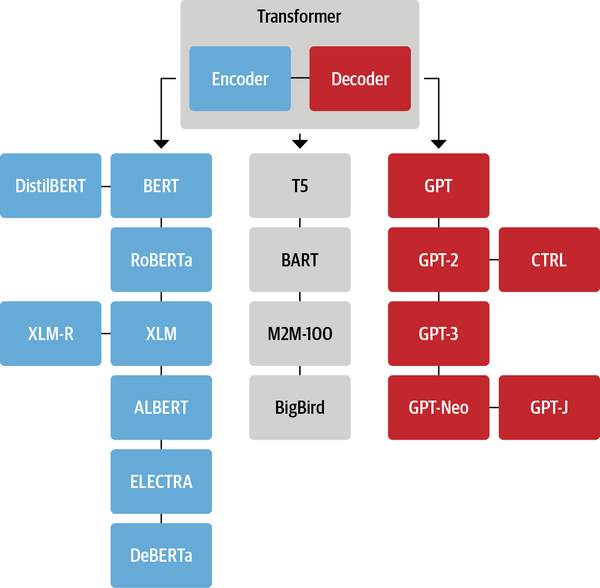
为了统一接口,我们先编写Encoder基类、Decoder基类。
编码器:
class Encoder(nn.Module):
"""编码器-解码器架构的基本编码器接口"""
def __init__(self, **kwargs):
super(Encoder, self).__init__(**kwargs)
def forward(self, X, *args):
raise NotImplementedError
解码器:
class Decoder(nn.Module):
"""编码器-解码器架构的基本解码器接口"""
def __init__(self, **kwargs):
super(Decoder, self).__init__(**kwargs)
def init_state(self, enc_outputs, *args):
raise NotImplementedError
def forward(self, X, state):
raise NotImplementedError
带注意力的解码器:
class AttentionDecoder(Decoder):
"""带有注意力机制解码器的基本接口"""
def __init__(self, **kwargs):
super(AttentionDecoder, self).__init__(**kwargs)
@property
def attention_weights(self):
raise NotImplementedError
编码器和解码器:
class EncoderDecoder(nn.Module):
"""编码器-解码器架构的基类"""
def __init__(self, encoder, decoder, **kwargs):
super(EncoderDecoder, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
def forward(self, enc_X, dec_X, *args):
enc_outputs = self.encoder(enc_X, *args)
dec_state = self.decoder.init_state(enc_outputs, *args)
return self.decoder(dec_X, dec_state)
2.8 编码器
Transformer的编码器由嵌入层、位置编码和多个相同的编码器层组成,
所以可以先实现一个编码器层:
class EncoderBlock(nn.Module):
"""Transformer编码器块"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
dropout, use_bias=False, **kwargs):
super(EncoderBlock, self).__init__(**kwargs)
self.attention = MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout,
use_bias)
self.addnorm1 = AddNorm(norm_shape, dropout)
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens, num_hiddens)
self.addnorm2 = AddNorm(norm_shape, dropout)
def forward(self, X, valid_lens):
Y = self.addnorm1(X, self.attention(X, X, X, valid_lens))
return self.addnorm2(Y, self.ffn(Y))
再加上嵌入层和位置编码,构成Transformer的编码器:
class TransformerEncoder(Encoder):
"""Transformer编码器"""
def __init__(self, vocab_size, key_size, query_size, value_size,
num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, num_layers, dropout, use_bias=False, **kwargs):
super(TransformerEncoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
self.embedding = nn.Embedding(vocab_size, num_hiddens)
self.pos_encoding = PositionalEncoding(num_hiddens, dropout)
self.blks = nn.Sequential()
for i in range(num_layers):
self.blks.add_module("block"+str(i),
EncoderBlock(key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, dropout, use_bias))
def forward(self, X, valid_lens, *args):
# 因为位置编码值在-1和1之间,
# 因此嵌入值乘以嵌入维度的平方根进行缩放,然后再与位置编码相加。
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
self.attention_weights = [None] * len(self.blks)
for i, blk in enumerate(self.blks):
X = blk(X, valid_lens)
self.attention_weights[i] = blk.attention.attention.attention_weights
return X
注意在位置编码的时候,根据嵌入维度进行了缩放。
这是因为如果不进行缩放,位置编码固定为-1到1,而原本数值的大小会受到嵌入维度大小的影响,数值不稳定。
2.9 解码器
和编码器类似,也是根据模型的结构图进行模块堆叠。 解码器层:
class DecoderBlock(nn.Module):
"""解码器中第i个块"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
dropout, i, **kwargs):
super(DecoderBlock, self).__init__(**kwargs)
self.i = i
self.attention1 = MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout)
self.addnorm1 = AddNorm(norm_shape, dropout)
self.attention2 = MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout)
self.addnorm2 = AddNorm(norm_shape, dropout)
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens, num_hiddens)
self.addnorm3 = AddNorm(norm_shape, dropout)
def forward(self, X, state):
enc_outputs, enc_valid_lens = state[0], state[1]
# 训练阶段,输出序列的所有词元都在同一时间处理,
# 因此state[2][self.i]初始化为None。
# 预测阶段,输出序列是通过词元一个接着一个解码的,
# 因此state[2][self.i]包含着直到当前时间步第i个块解码的输出表示
if state[2][self.i] is None:
key_values = X
else:
key_values = torch.cat((state[2][self.i], X), axis=1)
state[2][self.i] = key_values
if self.training:
batch_size, num_steps, _ = X.shape
# dec_valid_lens的开头:(batch_size,num_steps),
# 其中每一行是[1,2,...,num_steps]
dec_valid_lens = torch.arange(1, num_steps + 1, device=X.device).repeat(batch_size, 1)
else:
dec_valid_lens = None
# 自注意力
X2 = self.attention1(X, key_values, key_values, dec_valid_lens)
Y = self.addnorm1(X, X2)
# 编码器-解码器注意力。
# enc_outputs的开头:(batch_size,num_steps,num_hiddens)
Y2 = self.attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)
Z = self.addnorm2(Y, Y2)
return self.addnorm3(Z, self.ffn(Z)), state
解码器层有几个地方需要注意:
- 第一个自注意力是Masked Multi-head Attention,这是因为我们在训练的时候是把完整的结果输入给编码器,为了保证自回归性,不能让他在预测当前词的时候看到未来的信息,需要把未来的词mask掉。对应的代码在
dec_valid_lens = torch.arange(1, num_steps + 1, device=X.device).repeat(batch_size, 1),指定了计算每个token时的有效长度,让计算该token的注意力的时候看不到未来的token。 - 第二个注意力是Encoder-Decoder Attention,把编码器的最终输出作为Key-Value Pair输入到解码器每一层的第二个注意力头,而编码器作为Query。
- 训练的时候是一次性计算每个句子每个位置的attention,全部并行计算,而在预测的时候则是逐个token进行预测,因此使用了个state[2][self.i]存储了直到当前时间步第i个块解码的输出表示。因此会看到第一个Attention的QKV分别是X, key_values, key_values,在训练的时候key_values = X,而在预测的时候X是当前token,key_values还存储了之前的token。
解码器:
class TransformerDecoder(AttentionDecoder):
def __init__(self, vocab_size, key_size, query_size, value_size,
num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, num_layers, dropout, **kwargs):
super(TransformerDecoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
self.num_layers = num_layers
self.embedding = nn.Embedding(vocab_size, num_hiddens)
self.pos_encoding = PositionalEncoding(num_hiddens, dropout)
self.blks = nn.Sequential()
for i in range(num_layers):
self.blks.add_module("block"+str(i),
DecoderBlock(key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, dropout, i))
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
return [enc_outputs, enc_valid_lens, [None] * self.num_layers]
def forward(self, X, state):
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
self._attention_weights = [[None] * len(self.blks) for _ in range (2)]
for i, blk in enumerate(self.blks):
X, state = blk(X, state)
# 解码器自注意力权重
self._attention_weights[0][i] = blk.attention1.attention.attention_weights
# “编码器-解码器”自注意力权重
self._attention_weights[1][i] = blk.attention2.attention.attention_weights
return self.dense(X), state
@property
def attention_weights(self):
return self._attention_weights
3 训练和预测
训练:
num_hiddens, num_layers, dropout, batch_size, num_steps = 32, 2, 0.1, 64, 10
lr, num_epochs, device = 0.005, 200, d2l.try_gpu()
ffn_num_input, ffn_num_hiddens, num_heads = 32, 64, 4
key_size, query_size, value_size = 32, 32, 32
norm_shape = [32]
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = TransformerEncoder(
len(src_vocab), key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
num_layers, dropout)
decoder = TransformerDecoder(
len(tgt_vocab), key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
预测
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, dec_attention_weight_seq = d2l.predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device, True)
print(f'{eng} => {translation}, ',
f'bleu {d2l.bleu(translation, fra, k=2):.3f}')

